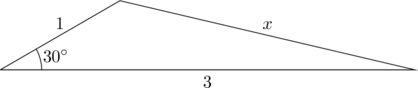
問題:上の図の![]() の値を求めよ。
の値を求めよ。
問題に「
 の値を求めよ」とあるが、そもそも
の値を求めよ」とあるが、そもそも の値は1つに決まるのだろうか? 実は、この三角形は、”2辺とその間の角”が与えられているため、三角形の合同条件に当てはめることができ、全ての辺の長さと角の大きさはただ一つの値に決まる。したがって、
の値は1つに決まるのだろうか? 実は、この三角形は、”2辺とその間の角”が与えられているため、三角形の合同条件に当てはめることができ、全ての辺の長さと角の大きさはただ一つの値に決まる。したがって、 の値もただ1つの値に決まっていて(下に証明を載せる)、求めることができる。実際に、定規や分度器を使ってこの三角形を紙の上に描き、定規で長さを測ればおおよその値を知ることができるだろう。
の値もただ1つの値に決まっていて(下に証明を載せる)、求めることができる。実際に、定規や分度器を使ってこの三角形を紙の上に描き、定規で長さを測ればおおよその値を知ることができるだろう。そのようにして定規で長さを測って求めてもよいのだが、このページでの目的は計算でその長さ
 を求めてみよう、ということである。
を求めてみよう、ということである。第一の解答として、三平方の定理を多用した解答を紹介する。第二の解答として、余弦定理(よげんていり)というものを使った解答を紹介する。この定理を使えば、簡単に
 の値を求めることができる。その後に、余弦定理の証明をいくつかあげる。
の値を求めることができる。その後に、余弦定理の証明をいくつかあげる。このページの構成は以下のようになる。
解答
(1)角度と辺の長さがわかる三角形を利用した解答。
(2)余弦定理を使った解答。余弦定理の証明
(3)第一余弦定理を使った証明。
(4)直角三角形を使った証明。
(5)座標を使った証明。
(6)ベクトルを使った証明。
 の値がただ1つに決まることの証明
の値がただ1つに決まることの証明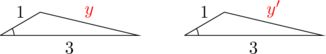
(証明)
問題の
 のとりえる値が、2つ以上(あるいは無数に)存在する、とする。・・・・・・前提
のとりえる値が、2つ以上(あるいは無数に)存在する、とする。・・・・・・前提
前提
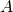 が成り立つとすると、
が成り立つとすると、 に異なる値、
に異なる値、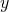 ,
, 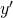 をとることができる。すなわち、
をとることができる。すなわち、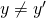 とすることができる。ところで、上の2つの三角形は、”2つの辺の長さとその間の角がそれぞれ等しい”ので、合同、すなわち、対応する全ての辺の長さと角の大きさがそれぞれ等しい三角形である。したがって、
とすることができる。ところで、上の2つの三角形は、”2つの辺の長さとその間の角がそれぞれ等しい”ので、合同、すなわち、対応する全ての辺の長さと角の大きさがそれぞれ等しい三角形である。したがって、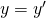 が導ける。
が導ける。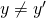 と、
と、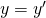 は、同時に成り立つことはできない。すなわち、矛盾であり、これは、前提
は、同時に成り立つことはできない。すなわち、矛盾であり、これは、前提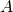 が間違っていたからである。したがって、
が間違っていたからである。したがって、 のとりえる値の数は、前提
のとりえる値の数は、前提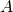 の否定をとって、1つ、もしくは、0である。・・・・・・(i)
の否定をとって、1つ、もしくは、0である。・・・・・・(i)一直線上にない3点は、それぞれの点を頂点として三角形を作ることができるため、この三角形は存在する。したがって、
 の値は、1つ以上(あるいは無数に)存在する。・・・・・・(ii)
の値は、1つ以上(あるいは無数に)存在する。・・・・・・(ii)(i)と(ii)より、
 はただ1つの値に決まる。
はただ1つの値に決まる。(証明終わり)
・角の大きさ
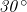 を利用するために、有名直角三角形の比を利用する。
を利用するために、有名直角三角形の比を利用する。
・三平方の定理を利用するために、頂点から垂線を下ろし、直角三角形を作る。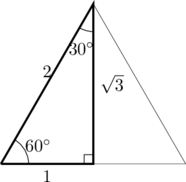
全ての辺の長さが
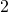 の正三角形を半分に切ってできる、右図のような三角形を考える。(太線の三角形を考える)
の正三角形を半分に切ってできる、右図のような三角形を考える。(太線の三角形を考える)すべての辺の長さを求める。2つの辺は、
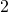 ,
,  とすぐにわかる。
とすぐにわかる。残りの辺の長さは、三平方の定理を使って、
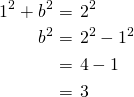
となるから、二乗して
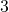 になるような数、すなわち、
になるような数、すなわち、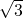 とわかる。(
とわかる。(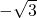 も二乗して
も二乗して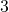 になるが、辺の長さを考えているので、
になるが、辺の長さを考えているので、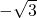 は不適)
は不適)この
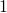 ,
,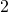 ,
,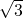 の比を利用して、上の問題を解く。
の比を利用して、上の問題を解く。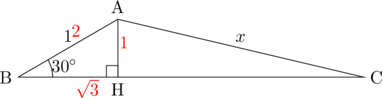
図のように頂点を
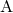 ,
, 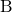 ,
,  とそれぞれおく。頂点
とそれぞれおく。頂点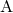 から辺
から辺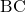 への垂線を引くと、一つの角が
への垂線を引くと、一つの角が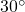 の直角三角形が現れる。(交点を
の直角三角形が現れる。(交点を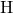 とおく)
とおく)ここで、先ほど求めた比が使える。辺
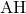 は、辺
は、辺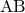 の
の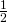 倍だから、
倍だから、
また、辺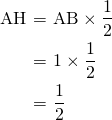
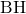 は辺
は辺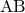 の
の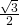 倍だから、
倍だから、
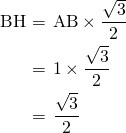
とでき、辺
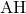 、辺
、辺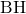 の長さが求まった。
の長さが求まった。辺
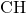 の長さは、辺
の長さは、辺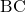 の長さが
の長さが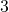 だったので、
だったので、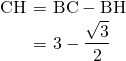
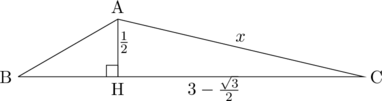
後は、三平方の定理を使って、
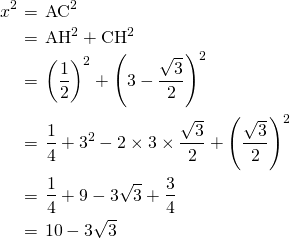
 は正だから、
は正だから、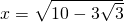 ・・・・・・(答え)
・・・・・・(答え)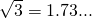 だから、この値を使うと、
だから、この値を使うと、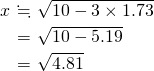
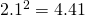 ,
, 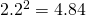 なので、
なので、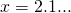 で、
で、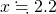
三平方の定理(ピタゴラスの定理)
右の図のように、直角三角形で、斜辺の長さを
 , それ以外の辺の長さを
, それ以外の辺の長さを ,
, 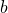 とおくと、次の式が成り立つ。
とおくと、次の式が成り立つ。![Rendered by QuickLaTeX.com \[c^{2} = a^{2} + b^{2}\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-810123da5ca8280fa950a1b687242dd8_l3.png)
・余弦定理
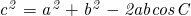 を利用する。この式に当てはめるだけで答えが出る。
を利用する。この式に当てはめるだけで答えが出る。余弦定理を使えば、
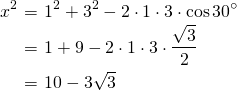
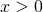 より、
より、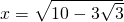 ・・・・・・(答え)
・・・・・・(答え)ドット”
 “は、積(掛け算)を表す。”
“は、積(掛け算)を表す。” “に同じ。
“に同じ。
余弦定理
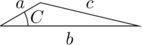
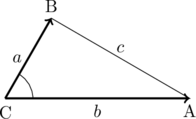
右の図の三角形において、次の式がなりたつ。
![Rendered by QuickLaTeX.com \[c^{2} = a^{2} + b^{2} - 2ab \cos{C}\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-94256e7e2c6789745c5932373732bf48_l3.png)
-
第一余弦定理による、第二余弦定理の証明
・第一余弦定理の3つの式を使う。
・1つの式に対して、2つの式を使い、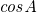 ,
, 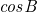 の2つを消去する。
の2つを消去する。
(証明)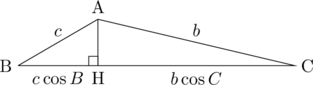
上の図より、
![Rendered by QuickLaTeX.com \[a = b \cos{C} + c \cos{B}\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-ccb94143eb8a5345dbffc7e35c07bdfe_l3.png)
これを第一余弦定理という。(
 は辺BCの長さ。この定理は、
は辺BCの長さ。この定理は、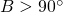 のときや、
のときや、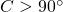 のときも成り立つ)
のときも成り立つ)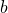 ,
,  についても同様の式が作れる。
についても同様の式が作れる。(1)
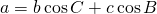
(2)
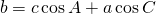
(3)
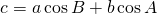
(3)
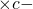 (1)
(1)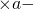 (2)
(2)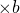 によって、
によって、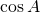 ,
, 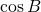 を消去する。
を消去する。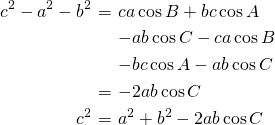
(証明終わり)
-
直角三角形を作った余弦定理の証明
・三平方の定理を利用するため、頂点
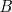 から対辺
から対辺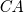 へ垂線を引き、直角三角形を作る。
へ垂線を引き、直角三角形を作る。
(証明)
(i)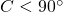 のとき
のとき
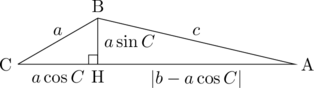 (ii)
(ii)上の図を考える。
三角形
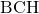 に注目して、
に注目して、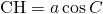 ,
, 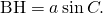 さらに、
さらに、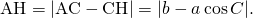 (絶対値記号を入れたのは、頂点
(絶対値記号を入れたのは、頂点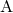 が点
が点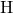 よりも左側にある場合、
よりも左側にある場合、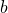 と、
と、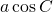 との大小関係がこの図と逆になり、
との大小関係がこの図と逆になり、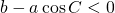 になってしまうため)
になってしまうため)次に、三角形
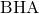 に注目して、三平方の定理を用いると、
に注目して、三平方の定理を用いると、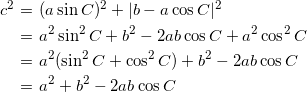
(
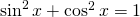 を使った)
を使った)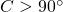 のとき
(iii)
のとき
(iii)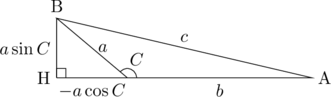
上の図を考える。
三角形
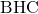 に注目して、
に注目して、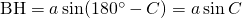 ,
, 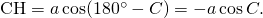 さらに、
さらに、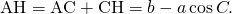
あとは、
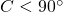 のときと同様に、
のときと同様に、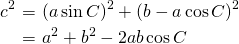
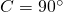 のとき
のとき
三平方の定理より、
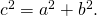 かつ、
かつ、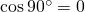 なので、
なので、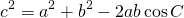
は成り立つ。
(i), (ii), (iii)より、全ての場合で、
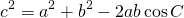
は成り立つ。
(証明終わり)
-
座標を使った余弦定理の証明
・頂点をxy座標上に設置し、頂点間の距離をとることにより求める。
(証明)
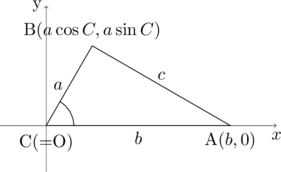
上の図のように、座標を置けば、
(頂点
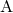 の座標)
の座標)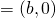
(頂点
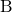 の座標)
の座標)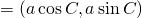
(頂点
 の座標)
の座標)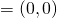
となる。
これを用いると、頂点
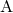 から頂点
から頂点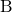 までの距離
までの距離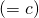 の自乗は、
の自乗は、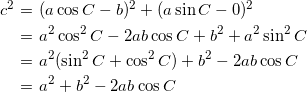
(
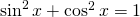 を使った)
を使った)(証明終わり)
-
ベクトルを使った余弦定理の証明
・平面上の図形なので、全てのベクトルを、2本のベクトルで表すことを目標にする。
(証明)
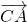 と
と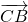 とを使って、
とを使って、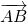 を表す。ここで、
を表す。ここで、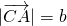 ,
, 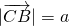 ,
, 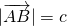 である。
である。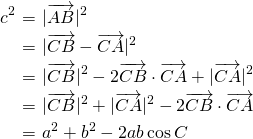
(証明終わり)