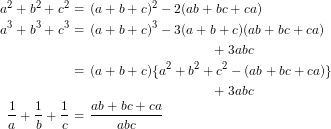問題:二次方程式![]() の2つの解を
の2つの解を![]() ,
, ![]() とするとき、次の式の値を求めよ。
とするとき、次の式の値を求めよ。
(1)![]()
(2)![]()
-
解答として次の2つをあげる。
(i)二次方程式の解の公式を使って
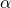 ,
, 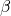 の値を求める方法。
の値を求める方法。
(ii)解と係数の関係を使って式の値を求める方法。また付録として次の2つを載せる。
(1)2つの文字を含む対称式の変形例
(2)三次方程式の解と係数の関係・3つの文字を含む対称式の変形例 -
二次方程式の解の公式を使う方法
次の方程式の解の公式を使って
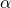 ,
, 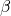 の値を具体的に求める。
の値を具体的に求める。二次方程式
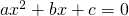 の解は、
の解は、![Rendered by QuickLaTeX.com \[x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-28c6d02783f9c708a7afc9605416e0ea_l3.png)
である。
求める式は
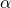 と
と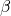 を入れ替えても同じ式になる。(このような式のことを対称式という。)したがって、
を入れ替えても同じ式になる。(このような式のことを対称式という。)したがって、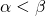 としても答えは変わらない。
としても答えは変わらない。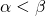 として、解を求めると、
として、解を求めると、![Rendered by QuickLaTeX.com \[\alpha=\cfrac{-3-\sqrt{11}}{2}\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-1c2ce9132cdfa1e6a46b5459cb3d1993_l3.png)
![Rendered by QuickLaTeX.com \[\beta=\cfrac{-3+\sqrt{11}}{2}\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-ccc8a6087c9c1e39ef9996a1a1f237e5_l3.png)
となる。
これを、求める式に代入すると、
(1)
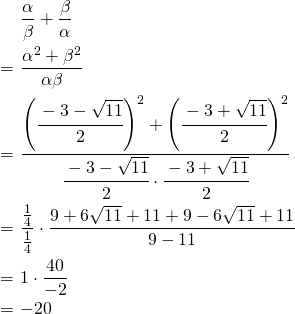
(2)
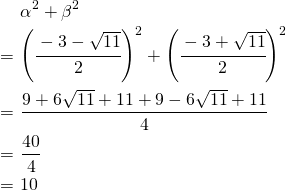
-
解と係数の関係を使って式の値を求める方法
求める式は対称式(文字を入れ替えても同じ式に戻る式)であり、解と係数の関係を使った解答が可能である。
二次方程式
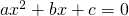 と、解
と、解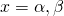 を持つ二次方程式
を持つ二次方程式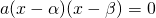 の係数を比較することにより、
の係数を比較することにより、 ,
, 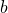 ,
,  と、
と、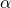 ,
, 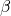 との間の関係式を導くことが出来る。
との間の関係式を導くことが出来る。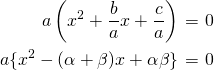
係数を比較して、
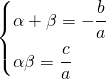
この問題の値を代入すると、
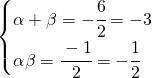
この数値を使って与えられた式の値を求める。
(1)
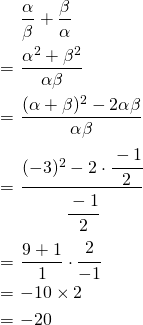
(2)
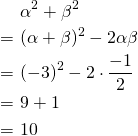
この方法の場合、
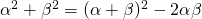 とするところが難しいが、知っておけば簡単である。
とするところが難しいが、知っておけば簡単である。二次方程式の解と係数の関係
二次方程式
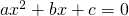 が、解
が、解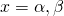 を持つとき、解と係数の間には次の関係が成り立つ。
を持つとき、解と係数の間には次の関係が成り立つ。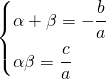
-
2つの文字を含む対称式の変形例
以下は
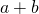 の値と
の値と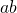 の値が与えられているとき、その値から対称式の値を求めるための変形である。
の値が与えられているとき、その値から対称式の値を求めるための変形である。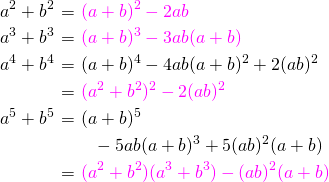
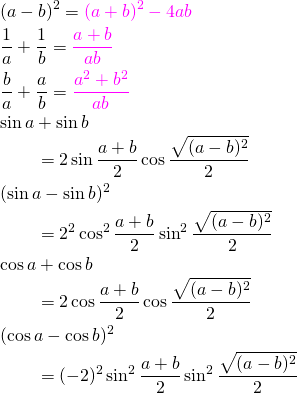
赤色で記した変形式はよく使われる。しかし、これらの変形式はすぐに導きだせるので覚える必要はまったくない。
また、上記のように綺麗に変形できない場合でも、
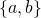 の値を求めることが出来るので、対称式の値を求めることが出来る。
の値を求めることが出来るので、対称式の値を求めることが出来る。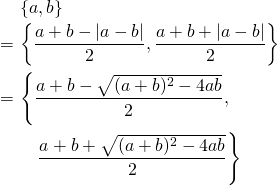
(注:上記の
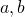 は、”
は、” と
と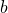 を要素として持つ集合”を意味する。上の式では”(集合)=(集合)”としているが、
を要素として持つ集合”を意味する。上の式では”(集合)=(集合)”としているが、 ,
, 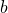 の大小関係が定まらないため、このようにしている。このように書けば、
の大小関係が定まらないため、このようにしている。このように書けば、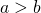 の場合にも
の場合にも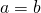 の場合にも対応できる。)
の場合にも対応できる。)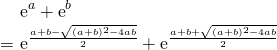
-
三次方程式の解と係数の関係
二次以上の方程式の場合も、係数比較により解と係数の関係を求めることが出来る。
三次方程式
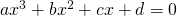 と、
と、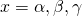 を解に持つ三次方程式
を解に持つ三次方程式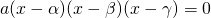 の係数を比較する。
の係数を比較する。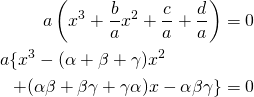
この二つの方程式の係数を比較すると、次の関係式を得る。
三次方程式の解と係数の関係
三次方程式
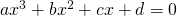 が、解
が、解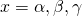 を持つとき、係数
を持つとき、係数 ,
, 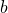 ,
,  ,
, 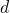 と、解
と、解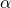 ,
, 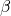 ,
, 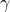 との間には次の関係が成り立つ。
との間には次の関係が成り立つ。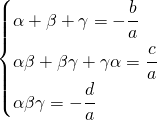
3つの文字を含む対称式の変形例
以下は
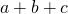 の値と、
の値と、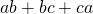 の値と
の値と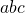 の値が与えられているとき、その値から対称式の値を求めるための変形例である。
の値が与えられているとき、その値から対称式の値を求めるための変形例である。