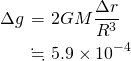問題:1.0mの高さから物を落としたとき、落下時間はどれほどかかるか。また2.0mのときは、どれほどかかるか。
問題の落下する時間は測定できるのだから、実際に測定してみればよい。
この問題のように、速度をつけずに(下に投げたりせずに)落下させる運動のことを、自由落下という。
このページでは、まず、実験によって落下する距離と落下時間との間にある関係を求める。次に、実験によって求めた距離と時間の式から、速度と時間、加速度と時間の式を求める。さらに、運動方程式を使って、物体に加わる力から、実験で求めた順とは逆に、加速度と時間の式、速度と時間の式、距離と時間の式を求める。最後に、地球上で重力加速度を測定するとき、場所や時間によって、どれほど変わるかを考える。
このページの構成は以下のようになる。
(1)落下時間の測定・距離と時間の式の導出
(2)速度と加速度
(3)運動方程式
(4)地球上での重力加速度
-
落下時間の測定
配線をハサミで切ることで落下させ、アルミ箔で作ったスイッチが押されるまでの時間を測定した。
動画:
結果:(見出しの数字は落下させた距離(m:メートル), 表中の数字は落下にかかった時間(ms:ミリ秒,千分の一秒))
0.100 0.200 0.300 0.400 0.500 1回目 144 200 247 275 323 2回目 136 191 243 282 320 3回目 143 196 244 290 317 4回目 151 202 249 286 308 5回目 138 200 246 272 321 0.600 0.700 0.800 0.900 1.000 1回目 351 383 401 426 453 2回目 351 378 399 430 452 3回目 350 381 407 429 460 4回目 356 376 407 428 460 5回目 351 374 403 428 451 1.100 1.200 1.300 1.400 1.500 1回目 474 495 518 538 553 2回目 470 500 514 536 557 3回目 479 500 519 536 557 4回目 475 494 521 535 555 5回目 471 496 510 538 553 1.600 1.700 1.800 1.900 2.000 1回目 573 588 602 621 646 2回目 569 591 600 621 646 3回目 574 588 604 601 634 4回目 573 584 607 616 643 5回目 573 575 595 619 643 距離と時間の式の導出
落下時間の値として、5回の実験結果の中央値を計算に使う。例えば、0.100mから落下させたときの落下時間は、小さい順から並べた測定値が136,138,143,144,151なので、中央にある143msを計算に使う。中央値を使う理由は、実験装置自体の精度がよく本来の誤差はものすごく小さいと考えるからである。ハサミできれいに切れなかったなど、ある一つの要因で大きく誤差が出る。中央値を使うことで、誤差が含まれている測定値を捨て、誤差が比較的出ていないと考えることのできる測定値を採用することができる。
下の図は、xt座標上に中央値をプロットしたものである(青の点)。
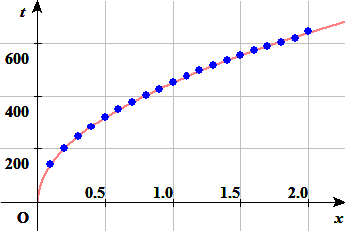
グラフの赤の曲線の式を求めたい。すなわち、プロットした点の近くを通る曲線の式を求めたい。
ここで、
 (落下距離)と
(落下距離)と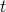 (落下時間)との関係式が、
(落下時間)との関係式が、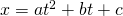 ・・・・・・(式A)で表されると仮定する(
・・・・・・(式A)で表されると仮定する( ,
, 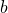 ,
,  は適当な定数)。
は適当な定数)。注:
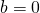 ,
, 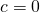 としない理由。
としない理由。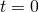 のとき(すなわち落下が始まっていないとき)、移動距離
のとき(すなわち落下が始まっていないとき)、移動距離 は
は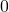 なので、
なので、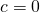 . また、この式を微分して、速度と時間の式を求めると、
. また、この式を微分して、速度と時間の式を求めると、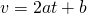 .
.  のとき、速度
のとき、速度 は
は なので、
なので、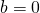 . このように考えて、
. このように考えて、 ,
,  としてもよい。しかし、測定装置の不備により常に距離が短めになっている場合や、常に測定時間が本来の時間よりも短くなっているといった場合が考えられる。この点を考慮するため、定数
としてもよい。しかし、測定装置の不備により常に距離が短めになっている場合や、常に測定時間が本来の時間よりも短くなっているといった場合が考えられる。この点を考慮するため、定数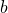 ,
,  を
を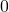 とせずに計算する。
とせずに計算する。式A:
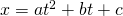 の定数をを最小二乗法により求める。
の定数をを最小二乗法により求める。高さ
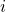 から落としたときの、落下距離を
から落としたときの、落下距離を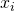 , 落下時間を
, 落下時間を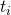 とおく(落下距離は中央値を使う)。例えば、0.100mから落下させたときは、
とおく(落下距離は中央値を使う)。例えば、0.100mから落下させたときは、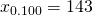 ,
, 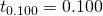 となる。
となる。落下時間が
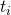 のとき、式Aにより落下距離の理論値
のとき、式Aにより落下距離の理論値 を求めると
を求めると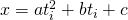 となる。この理論値
となる。この理論値 と中央値
と中央値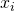 との距離が短ければ短いほどよい。そこで、
との距離が短ければ短いほどよい。そこで、 と
と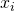 の差
の差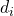 の二乗、すなわち
の二乗、すなわち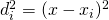 をとる。全ての高さ
をとる。全ての高さ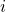 に対して
に対して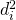 を求め、その和
を求め、その和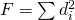 が最小になるような
が最小になるような ,
, 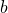 ,
,  を求める。
を求める。注:
 と中央値
と中央値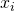 との差を小さくしたいのだから、単に、
との差を小さくしたいのだから、単に、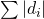 が最小となる
が最小となる ,
, 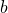 ,
,  を求めてもよいのだが、二乗して絶対値をはずしたほうが計算が簡単である。二乗の和でずれを評価すると、大きくずれているところが少なくなるというメリットもある。
を求めてもよいのだが、二乗して絶対値をはずしたほうが計算が簡単である。二乗の和でずれを評価すると、大きくずれているところが少なくなるというメリットもある。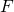 が最小となるには、
が最小となるには、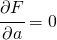 ,
, 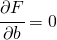 ,
, 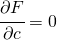 が必要である。(
が必要である。(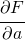 は、偏微分を表す記号で、
は、偏微分を表す記号で、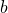 ,
,  は固定して
は固定して で微分する、という意味)
で微分する、という意味)したがって、
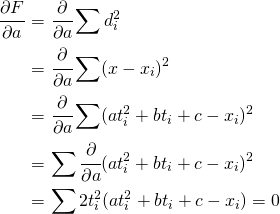
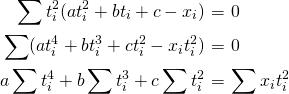
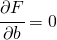 ,
, 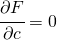 についても同様に計算すると、次の三元連立一次方程式が得られる。(この方程式を最小二乗放物線に対する正規方程式という)
についても同様に計算すると、次の三元連立一次方程式が得られる。(この方程式を最小二乗放物線に対する正規方程式という)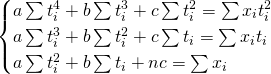
(ただし、
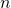 は
は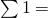 (
(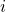 の個数))
の個数))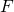 とそれを微分した関数は連続関数であり、
とそれを微分した関数は連続関数であり、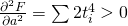 ,
, 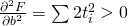 ,
, 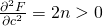 であるから、極値は上の連立方程式を満たす一組しかなく、極値は最小値になっていることがわかる。
であるから、極値は上の連立方程式を満たす一組しかなく、極値は最小値になっていることがわかる。この連立方程式を解くと、
 ,
, 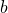 ,
,  の値が得られる。
の値が得られる。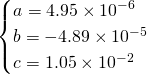
これで、
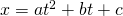 の関係式を求めることができた。上図の赤の曲線はこの式のグラフである。
の関係式を求めることができた。上図の赤の曲線はこの式のグラフである。この式を
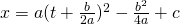 により
により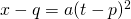 の形に変形すると、
の形に変形すると、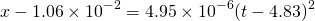
実際の落下距離を
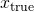 , 実際の落下時間を
, 実際の落下時間を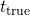 とすると、
とすると、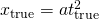 という関係になるはずである。これと上の式をくらべることにより、実際の落下時間は、測定値よりも5msほど短かったと推測できる。また、実際の落下距離は、測定値よりも1cmほど短かったと推測できる。
という関係になるはずである。これと上の式をくらべることにより、実際の落下時間は、測定値よりも5msほど短かったと推測できる。また、実際の落下距離は、測定値よりも1cmほど短かったと推測できる。測定値のずれを省き、msをsに書き直すと、次のようになる。
実験のまとめ
落下する距離
 (m)と落下する時間
(m)と落下する時間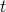 (s)との間には、
(s)との間には、(1)
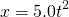
という関係がある。
(実験の値より、)1.0mの高さから物を落下させると、落下時間は、およそ0.45秒。2.0mの高さから物を落下させると、およそ0.64秒かかる。・・・・・・(答え)
参考:OpenOfficeのCalcファイル -
速度と加速度
(1)式より、
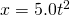 . ここで
. ここで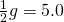 とおくと、
とおくと、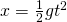 となる。(この定数
となる。(この定数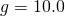 は重力加速度と呼ばれる。重力加速度
は重力加速度と呼ばれる。重力加速度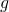 は測定場所によって変化するが、標準重力加速度というものが定められており、普通はその値を使う。標準重力加速度の値は、
は測定場所によって変化するが、標準重力加速度というものが定められており、普通はその値を使う。標準重力加速度の値は、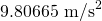 である。)
である。)速度
 は、落下距離
は、落下距離 を時間微分すれば求まるので、次のようになる。
を時間微分すれば求まるので、次のようになる。![Rendered by QuickLaTeX.com \[v=\frac{dx}{dt}=gt\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-16a9d83a0e61048733389caba4efb46f_l3.png)
これは、時間
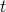 のときの瞬間の速度が
のときの瞬間の速度が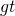 になる、ということである。この式より、1秒後の瞬間の速度は
になる、ということである。この式より、1秒後の瞬間の速度は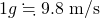 である。(
である。(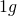 と書いたのは、単に
と書いたのは、単に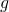 と書いたとき、単位
と書いたとき、単位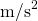 と読み間違えられるの恐れがあるため。
と読み間違えられるの恐れがあるため。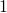 に1”秒”という意味を持たせ、誤読を防いでいる。)
に1”秒”という意味を持たせ、誤読を防いでいる。)瞬間の速度は平均の速度の極限である。瞬間の速度の意味がよくわからなければ、例えば次のように考える。1秒後から1.01秒後の平均の速度は、
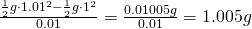 となる。時間幅を0.01→0.001→0.0001と小さくしていけば、平均の速度は、瞬間の速度
となる。時間幅を0.01→0.001→0.0001と小さくしていけば、平均の速度は、瞬間の速度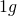 に近づいていく。(この瞬間の速度を求める操作が微分という操作である。)
に近づいていく。(この瞬間の速度を求める操作が微分という操作である。)加速度
 は、速度
は、速度 を時間微分すれば求まるので、次のようになる。
を時間微分すれば求まるので、次のようになる。![Rendered by QuickLaTeX.com \[a=\frac{dv}{dt}=g\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-51381c9ef1433ec9d5132ee639864d18_l3.png)
-
運動方程式
運動方程式(運動の第二法則)から、式(1):
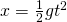 を求める。
を求める。ニュートンの運動方程式
物体の質量
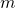 と、物体の加速度
と、物体の加速度 と、物体に加わる力
と、物体に加わる力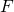 との関係は次の式で表される。
との関係は次の式で表される。![Rendered by QuickLaTeX.com \[ma=F\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-60bfaf13b222abda4e4b5863681045b9_l3.png)
加速度
 は、位置
は、位置 の二回微分と定義される。残りの質量
の二回微分と定義される。残りの質量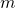 と力
と力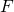 は初登場である。
は初登場である。物体には、その物体固有の質量
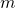 というものがある。質量
というものがある。質量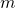 は、大きさしかもたない量である(方向を持たない。このような量をスカラーと呼ぶ)。もし力
は、大きさしかもたない量である(方向を持たない。このような量をスカラーと呼ぶ)。もし力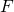 が一定であれば、質量
が一定であれば、質量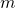 が大きいほど、加速度
が大きいほど、加速度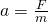 の大きさは小さくなる。
の大きさは小さくなる。力
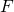 は、大きさと方向を持つベクトル量である。質量
は、大きさと方向を持つベクトル量である。質量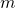 の物体が加速度
の物体が加速度 で運動していれば、そこには力
で運動していれば、そこには力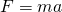 が働いている。
が働いている。運動方程式
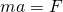 は次の役割を持つ。
は次の役割を持つ。(1)
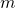 と
と と
と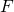 との関係を示す。
との関係を示す。
(2)力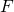 を定義する。
を定義する。
運動方程式が担う役割は多いのだが、とりあえずは、関係式
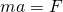 が使えればよい。
が使えればよい。落下する物体には加速度
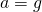 が発生する。したがって、力
が発生する。したがって、力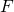 は運動方程式より、
は運動方程式より、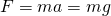 である。したがって、落下する物体には質量
である。したがって、落下する物体には質量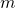 に比例した力が加わることがわかる。
に比例した力が加わることがわかる。
ここで、落下していない物体、すなわち、静止している物体にも力
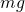 が加わっているとしたらどうだろう? しかし、物体に加わる力
が加わっているとしたらどうだろう? しかし、物体に加わる力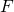 は、
は、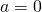 より、
より、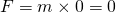 である。この場合、物体には、机などから
である。この場合、物体には、机などから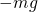 と力
と力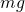 を打ち消す力が働いていると考える。このようにして、物体に加わる力の和(合力(ごうりょく))
を打ち消す力が働いていると考える。このようにして、物体に加わる力の和(合力(ごうりょく))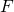 を
を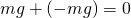 とする。運動方程式の力
とする。運動方程式の力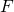 は物体に加わる力をすべて足し合わせた合力である。
は物体に加わる力をすべて足し合わせた合力である。さて、物体に力
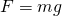 が加わっているとしよう。このとき、物体の加速度
が加わっているとしよう。このとき、物体の加速度 は、運動方程式より、
は、運動方程式より、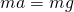 . したがって、
. したがって、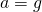 である。これを積分すれば速度
である。これを積分すれば速度 が得られる。
が得られる。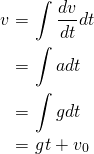
(
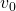 は積分定数。ここでは、
は積分定数。ここでは、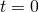 での速度(初速度)を表す)
での速度(初速度)を表す)ここから、さらに物体の位置
 を求めるには、速度
を求めるには、速度 を積分すればよい。
を積分すればよい。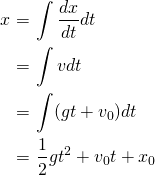
(
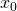 は積分定数。ここでは、
は積分定数。ここでは、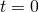 での位置を表す)
での位置を表す)実験では、初速度
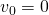 , 初期位置
, 初期位置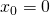 だったので、これを代入すると、
だったので、これを代入すると、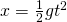 . 式(1)を運動方程式より求めることができた。
. 式(1)を運動方程式より求めることができた。 -
地球上での重力加速度
地球上で重力は、次の要因によって、場所や時間により異なる。
(
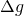 は重力加速度の最大誤差。単位:
は重力加速度の最大誤差。単位: 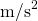 )
)(1)地球の自転。
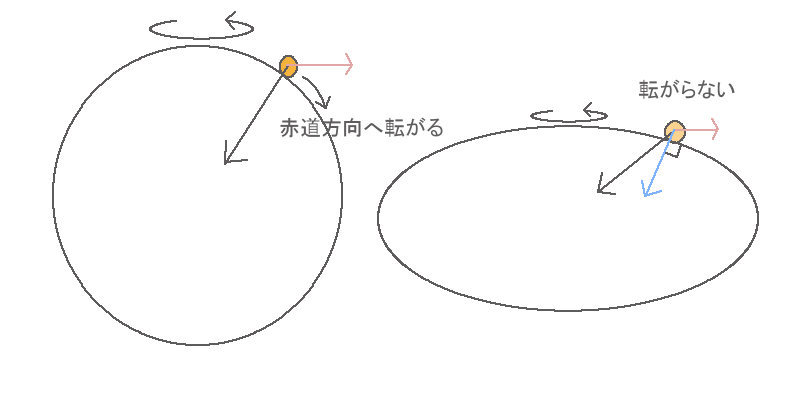
![Rendered by QuickLaTeX.com \[\Delta g=3.4\times10^{-2}\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-8709558999c497e65bd96c4729be154c_l3.png)
(2)標高。
![Rendered by QuickLaTeX.com \[\Delta g=2.7\times10^{-2}\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-fd6a84ff3f142f0090d8acddeb5f10e5_l3.png)
(3)地球が回転楕円体の形をしている。
![Rendered by QuickLaTeX.com \[\Delta g=1.8\times10^{-2}\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-ac05208b3e2df3a6ee4d8b2d3550743d_l3.png)
(4)地球内部の質量分布の不均一。
![Rendered by QuickLaTeX.com \[\Delta g=5.9\times10^{-4}\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-4f5c794be7a4a45b67ad72acd4a10110_l3.png)
(5)月。
![Rendered by QuickLaTeX.com \[\Delta g=1.1\times10^{-6}\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-669c5ed826b1a579566a6db3ff9951fa_l3.png)
(6)太陽。
![Rendered by QuickLaTeX.com \[\Delta g=5.0\times10^{-7}\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-b4c5b7b440353915f581809337b06fa4_l3.png)
(7)その他の天体。
![Rendered by QuickLaTeX.com \[\Delta g=10^{-12}\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-50c64a9ed0d4c36ceb9480ecbca24f83_l3.png)
この項目は、筆者が勉強中のため、未完成です。誤りが含まれていると思うので、あまり参考にはしないでください。次回更新日:未定。
(1)地球の自転
地球は、およそ1日(
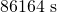 )で一回転(
)で一回転(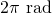 )している。地球上にいる観測者は、この自転による遠心力を感じることになる。遠心力による加速度は角速度を
)している。地球上にいる観測者は、この自転による遠心力を感じることになる。遠心力による加速度は角速度を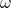 , 半径を
, 半径を とすると、
とすると、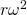 で与えられる。したがって、赤道上(赤道半径
で与えられる。したがって、赤道上(赤道半径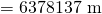 )で観測者が感じる遠心力による加速度は、
)で観測者が感じる遠心力による加速度は、
赤道上では、北極南極と比べると、この加速度
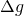 の分だけ重力を小さく感じる。
の分だけ重力を小さく感じる。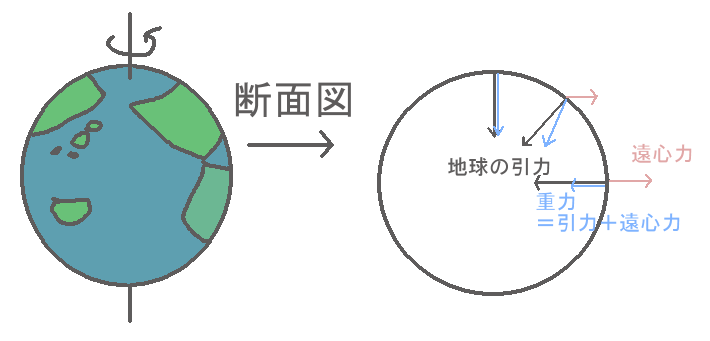
(2)標高
世界で一番高い山エベレストの標高
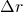 は、約
は、約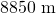 である。地球半径
である。地球半径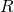 は約
は約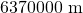 で、地心重力定数
で、地心重力定数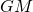 (万有引力定数
(万有引力定数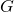 と地球の質量
と地球の質量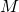 との掛け算)は約
との掛け算)は約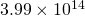 なので、
なので、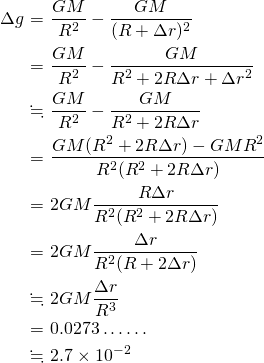
エベレストの山頂にいる人は、浜辺にいる人(=標高0m)に比べて、この加速度
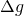 分だけ重力を小さく感じる。
分だけ重力を小さく感じる。1回目の
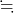 記号と2回目の
記号と2回目の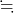 記号を書いた計算では、
記号を書いた計算では、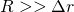 (
(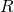 が
が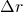 と比べて非常に大きい)を利用し、
と比べて非常に大きい)を利用し、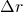 を含む項を消去している。1回目の計算では、
を含む項を消去している。1回目の計算では、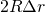 の項を消去していないが、これを消去すると最終的な答えが大きく変わるためである(消去してしまうと答えが
の項を消去していないが、これを消去すると最終的な答えが大きく変わるためである(消去してしまうと答えが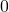 になる)。消してよいかの見極めが出来ない場合は、消さないでおいて、計算が進んで消してもよいと判断できた段階で消せばよい。2回目の
になる)。消してよいかの見極めが出来ない場合は、消さないでおいて、計算が進んで消してもよいと判断できた段階で消せばよい。2回目の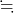 記号を書いた計算で、
記号を書いた計算で、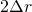 の項を消去しても答えはほとんど変わらないことは、具体的な数字を代入するなどして少し考えれば分かるだろう。
の項を消去しても答えはほとんど変わらないことは、具体的な数字を代入するなどして少し考えれば分かるだろう。(3)地球が回転楕円体
地球は真ん丸の球ではなく、すこしつぶれた形をしている。地球が完全な球であるとすると、地球上にある物体は遠心力により、赤道方向に引き寄せられてしまう。地球が回転楕円体の形をしているので、地球上にある物体は静止できる。
地球は赤道方向に膨らんでいるので、赤道上では地球の中心からの距離が大きくなる。したがって、赤道と極では、地球の中心からの距離が長い赤道上のほうが、重力が小さい。
この影響
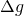 は、赤道における重力
は、赤道における重力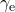 が
が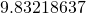 , 極における重力
, 極における重力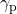 が
が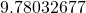 であるので、自転による重力加速度の影響を
であるので、自転による重力加速度の影響を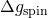 とすれば、
とすれば、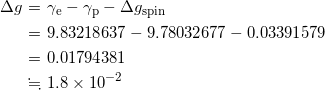
赤道上では、北極南極と比べると、この加速度
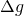 分だけ重力を小さく感じる。
分だけ重力を小さく感じる。(注)地球の質量分布を均一とみなし、地球の自転を考えると、地球の形は回転楕円体になる。(これを求める計算は高度になるため、今は解説しない。ヒント:ルジャンドル関数を使う。2014年末までにはこの計算の解説を公開するつもりである)
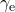 や
や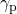 は正規重力とよばれるもので、地球を回転楕円体とし、さらに地球の自転による遠心力を考えたときの、重力である。
は正規重力とよばれるもので、地球を回転楕円体とし、さらに地球の自転による遠心力を考えたときの、重力である。
(4)地球内部の質量分布の不均一
地球には、凹凸があり内部構造も不均一であるため、地球を質量分布が均一な回転楕円体とみなした場合と比べて、重力分布に差がある。
もし地球に陸地がなく、全て海だったとしたときの海水面をジオイドという。ジオイドは等ポテンシャル面である(ジオイド上では重力一定)。地球内部の質量分布が不均一なため、ジオイドも回転楕円体と比べると、凹凸がある。
ジオイドと回転楕円体との間の高低差をジオイド高という。ジオイド高は
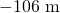 から
から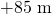 の値をとる。
の値をとる。したがって、質量分布の不均一による重力加速度への最大の影響
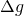 は、(2)標高での計算結果とジオイド差
は、(2)標高での計算結果とジオイド差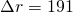 を利用して、
を利用して、