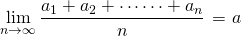問題:次の式の値を求めよ。
(1)![]()
(2)![]()
(3)![]()
(4)数列![]() が
が![]() の値に収束するときの、
の値に収束するときの、
![]()
-
このページでは、数列の極限値について考える。
数列の極限値を考えるということは、簡単に言えば、数列が最終的にどのような値に近づいていくか、ということを考えることである。例えば、(1)の問題は、
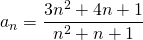 のとき、数列
のとき、数列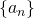 が、
が、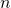 を無限に大きくしていくとき、どのような値に近づくか、ということを考えさせる問題である。
を無限に大きくしていくとき、どのような値に近づくか、ということを考えさせる問題である。この問題を解くために、ε-N論法(イプシロン-エヌろんぽう)で、極限値の定義を行い、基本定理の証明を行う。その後に、それぞれの問題について考える。
このページの構成は以下のようになる。
(1)数列の極限値の定義(ε-N論法)
(2)極限の基本定理
(3)問題の解答 -
ε-N論法による極限値の定義
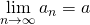 という式の意味は、”
という式の意味は、”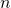 を限りなく大きくするとき、
を限りなく大きくするとき、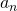 は値
は値 に限りなく近づく(もしくは一致する)”という意味である。例えば、
に限りなく近づく(もしくは一致する)”という意味である。例えば、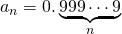 としたとき、
としたとき、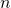 を大きくしていくと、
を大きくしていくと、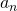 は
は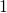 に限りなく近づく。このようなとき、
に限りなく近づく。このようなとき、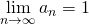 と書ける。ちなみに、
と書ける。ちなみに、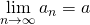 となるとき、数列
となるとき、数列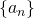 は
は に収束(しゅうそく)するという。
に収束(しゅうそく)するという。“限りなく大きく”や、”限りなく近づく”という言葉をそのまま使って、極限値の定理を証明するのは、難しい。この難しさを回避するために、ε-N論法(イプシロン-エヌろんぽう)という、不等式を使って極限を定義する方法が生まれた。ε-N論法のおかげで、微分積分学の基礎となる極限を厳密に定義することができ、微積を論理的に確かなものにすることができる。
ε-N論法による極限値の定義
数列
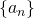 が数
が数 に収束するとは、すべての
に収束するとは、すべての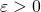 に対して、ある自然数
に対して、ある自然数 がとれて、自然数
がとれて、自然数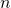 が
が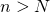 ならば
ならば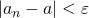 が成立する、ということである。
が成立する、ということである。もしくは、全称記号
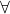 と存在記号
と存在記号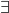 を使って次のようにも表せる。
を使って次のようにも表せる。論理記号を使った極限値の定義
数列
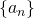 が数
が数 に収束するとは、次が成立するということである。
に収束するとは、次が成立するということである。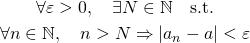
論理記号の読み方
上の論理記号の読み方を説明する。
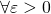 は、”すべての正である
は、”すべての正である (イプシロン)に対して”という意味である。
(イプシロン)に対して”という意味である。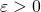 によって
によって の範囲を限定し、さらに全称記号
の範囲を限定し、さらに全称記号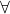 を付けることで、後に出てくる式はすべての(任意の)
を付けることで、後に出てくる式はすべての(任意の)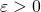 で成立するということを表している。
で成立するということを表している。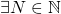 は、”後に書かれている式を満たす自然数
は、”後に書かれている式を満たす自然数 が存在する”という意味である。
が存在する”という意味である。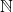 は自然数全体の集合を表す記号である。
は自然数全体の集合を表す記号である。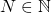 (
( は自然数の集合
は自然数の集合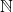 の要素であるという意味)と書くことで、
の要素であるという意味)と書くことで、 が自然数であることを表現している。これに存在記号
が自然数であることを表現している。これに存在記号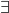 を付けることで、この後に続く式を満たす
を付けることで、この後に続く式を満たす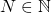 が存在することを表している。
が存在することを表している。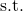 は、such thatの略で、”どのような”
は、such thatの略で、”どのような” が存在するかということを後の式が説明することを表している。
が存在するかということを後の式が説明することを表している。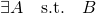 で、「BとなるようなAが存在する」という意味である。
で、「BとなるようなAが存在する」という意味である。 は、”すべての自然数
は、”すべての自然数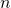 に対して”という意味である。
に対して”という意味である。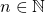 は
は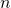 が自然数であることを表している。これに全称記号
が自然数であることを表している。これに全称記号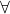 を付けることで、後に続く式がすべての自然数
を付けることで、後に続く式がすべての自然数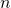 に対して成立することを表している。
に対して成立することを表している。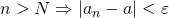 は、
は、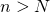 ならば
ならば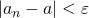 であることを表している。
であることを表している。以上のことを踏まえ上の論理記号を日本語に訳すると、先にあげた定義のようになる。
ε-N論法の考え方
ε-N論法では、任意の
 (イプシロン)とそれに対する適当な
(イプシロン)とそれに対する適当な の2つの変数が重要な役割を持っている。
の2つの変数が重要な役割を持っている。 は正の実数であれば何でもよいのだが、大きい
は正の実数であれば何でもよいのだが、大きい に興味があるのではなく、小さい
に興味があるのではなく、小さい に興味がある。
に興味がある。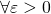 は、”どんなに小さい
は、”どんなに小さい に対しても”という意味なのである。そして、非常に小さい
に対しても”という意味なのである。そして、非常に小さい に対して、ある大きな
に対して、ある大きな を用意する。この大きな
を用意する。この大きな 以上の
以上の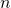 であれば、どんな
であれば、どんな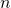 に対しても
に対しても の値と
の値と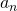 の値の距離(差の絶対値)が
の値の距離(差の絶対値)が より小さくできる。もし、このような
より小さくできる。もし、このような が、どんな小さな
が、どんな小さな に対しても用意できるのならば、十分に大きい
に対しても用意できるのならば、十分に大きい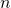 をとれば、
をとれば、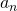 と
と との距離をいくらでも小さくできるといえるのだから、数列
との距離をいくらでも小さくできるといえるのだから、数列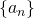 は数
は数 に収束するといえる。ε-N論法は、このような考え方である。
に収束するといえる。ε-N論法は、このような考え方である。例題
最後にε-N論法を使って問題を解こう。
問題:次の式の値を求めよ。
![Rendered by QuickLaTeX.com \[\lim_{n \to \infty} \frac{1}{n}\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-8a0ea0e6554fd4bbe73b81e7b20535c2_l3.png)
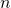 =10, 100, 1000…のとき、
=10, 100, 1000…のとき、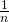 =0.1, 0.01, 0.001…となるから、
=0.1, 0.01, 0.001…となるから、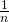 は
は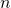 を大きくすると、
を大きくすると、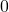 に近づくだろうと予想できる。
に近づくだろうと予想できる。(解答)
任意の
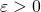 に対して、自然数
に対して、自然数 を、
を、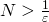 となるようにとることができる。このとき、すべての
となるようにとることができる。このとき、すべての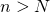 である自然数
である自然数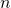 に対して、
に対して、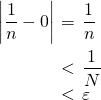
以上より、任意の
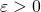 に対して、ある自然数
に対して、ある自然数 がとれ、自然数
がとれ、自然数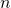 が
が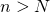 ならば、
ならば、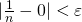 であるといえたので、
であるといえたので、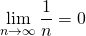 である。
である。(解答終わり)
-
基本定理
収束と有界
収束する数列は有界である。
有界であるとは、無限に大きくなったり無限に小さくなったりしない、ということである。例えば数列
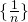 は有界である。0以上1以下の範囲に収まっている。しかし、数列
は有界である。0以上1以下の範囲に収まっている。しかし、数列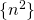 は有界ではない。いくらでも大きくなってしまう。数列
は有界ではない。いくらでも大きくなってしまう。数列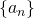 が、適当な数
が、適当な数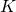 を用いて
を用いて と書ければ、数列
と書ければ、数列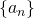 は有界である。例えば、数列
は有界である。例えば、数列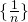 の場合、
の場合、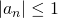 と書け、有界である。(
と書け、有界である。(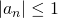 は、数列
は、数列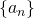 のすべての項が-1以上1以下に収まるという意味)
のすべての項が-1以上1以下に収まるという意味)(証明)
数列
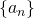 が数
が数 に収束するとする。このとき、ある自然数
に収束するとする。このとき、ある自然数 をとって、
をとって、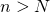 ならば
ならば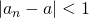 となるようにできる(
となるようにできる(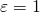 )。したがって、
)。したがって、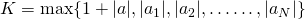 とすれば、
とすれば、 とできる。ゆえに、収束する数列は有界。
とできる。ゆえに、収束する数列は有界。(証明終わり)
極限の計算の基本定理
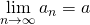 ,
, 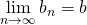 のとき、次の式が成り立つ。
のとき、次の式が成り立つ。(1)
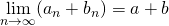
(2)
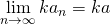 (ただし、
(ただし、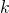 は定数)
は定数)(3)
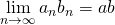
(4)
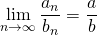 (ただし、
(ただし、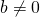 )
)注:下の証明を読む前に、三角不等式が分からない場合は下のほうにスクロールして、どのようなものか確認しておくこと。
(1)
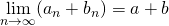
(証明)
任意の
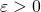 に対し、適当な自然数
に対し、適当な自然数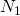 ,
, 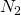 をとって、
をとって、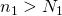 のとき
のとき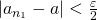 、
、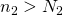 のとき
のとき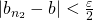 とできる。
とできる。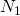 ,
, 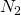 のうち大きいほうを
のうち大きいほうを をおけば、
をおけば、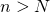 のとき
のとき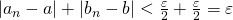 とできる。したがって、
とできる。したがって、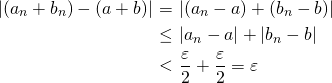
任意の
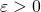 に対して、自然数
に対して、自然数 を、
を、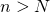 のとき
のとき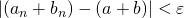 となるようにとることができたので、与式は成り立つ。
となるようにとることができたので、与式は成り立つ。(証明終わり)
(2)
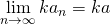 (ただし、
(ただし、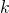 は定数)
は定数)(証明)
任意の
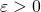 に対して、自然数
に対して、自然数 を、
を、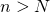 のとき、
のとき、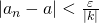 となるようにとることができる。このとき、
となるようにとることができる。このとき、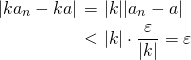
任意の
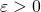 に対して、自然数
に対して、自然数 を、
を、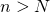 のとき
のとき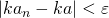 となるようにとることができたので、与式は成り立つ。
となるようにとることができたので、与式は成り立つ。(証明終わり)
(3)
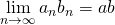
(証明)
数列
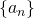 は収束するから有界であり、ある正の定数
は収束するから有界であり、ある正の定数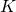 をとって、
をとって、 とすることができる。さらに、任意の
とすることができる。さらに、任意の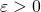 に対して、適当な自然数
に対して、適当な自然数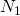 ,
, 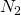 をとり、
をとり、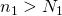 のとき
のとき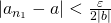 、
、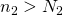 のとき
のとき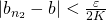 とすることができる。
とすることができる。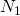 ,
, 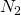 のうち大きいほうを
のうち大きいほうを にとり、
にとり、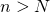 とすると次のように計算できる。
とすると次のように計算できる。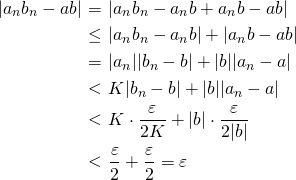
任意の
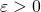 に対して、
に対して、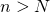 ならば
ならば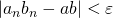 となるような自然数
となるような自然数 をとることができたので、与式は成り立つ。
をとることができたので、与式は成り立つ。(証明終わり)
(4)
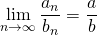 (ただし、
(ただし、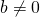 )
)(証明)
数列
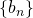 は数
は数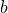 に収束し
に収束し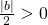 なので、十分大きな
なので、十分大きな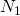 をとれば、
をとれば、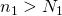 のとき
のとき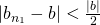 とできる。これを変形すると、
とできる。これを変形すると、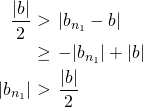
さらに、任意の
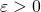 に対して、
に対して、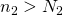 ならば
ならば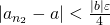 となるような自然数
となるような自然数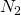 がとれ、また、
がとれ、また、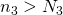 ならば
ならば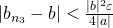 となるような
となるような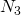 がとれる。これらの自然数
がとれる。これらの自然数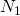 ,
, 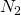 ,
, 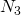 のうち一番大きいものを
のうち一番大きいものを とし、自然数
とし、自然数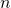 が
が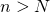 を満たすとすると次のように計算できる。
を満たすとすると次のように計算できる。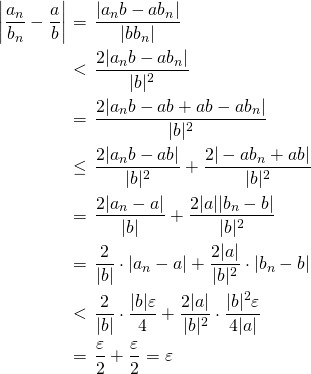
任意の
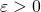 に対して、
に対して、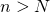 のとき
のとき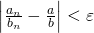 となるような自然数
となるような自然数 をとることができたので、与式は成り立つ。
をとることができたので、与式は成り立つ。(証明終わり)
三角不等式
任意の実数
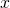 ,
, 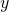 に対して次の式が成り立つ。
に対して次の式が成り立つ。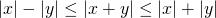
-
(1)の解答
・分母分子を次数の高い項で割ればよい。
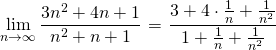
ここで、
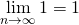 ,
, 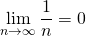 ,
, 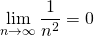 なので、
なので、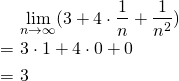
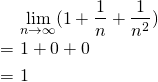
したがって、
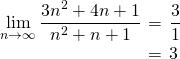
-
(2)の解答
・
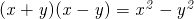 が利用できるように、分母(=1)と分子を操作する。
が利用できるように、分母(=1)と分子を操作する。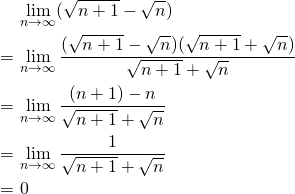
(
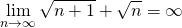 と下枠の定理を使った。)
と下枠の定理を使った。)無限大に発散する数列の逆数の極限
数列
 が無限大に発散するとき、
が無限大に発散するとき、![Rendered by QuickLaTeX.com \[\lim_{n \to \infty} \frac{1}{a_n}=0\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-4a42ae6022fe237647380fdee73888f5_l3.png)
数列
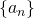 が無限大に発散するとは、
が無限大に発散するとは、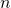 を大きくとれば
を大きくとれば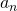 の値をいくらでも大きくできるということである。このとき、
の値をいくらでも大きくできるということである。このとき、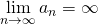 と書く。収束しない数列(極限値が定まらない数列)のことを発散する数列という。
と書く。収束しない数列(極限値が定まらない数列)のことを発散する数列という。数列の発散をε-N論法で書くと次のようになる。
無限大に発散するということの定義
数列
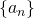 が無限大に発散するとは、次が成立するということである。
が無限大に発散するとは、次が成立するということである。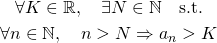
ただし、
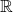 は実数全体の集合を表す記号。
は実数全体の集合を表す記号。この定義を使って、上枠の定理を証明しよう。
(証明)
数列
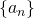 は無限大に発散するので、任意の
は無限大に発散するので、任意の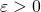 に対して、
に対して、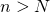 ならば
ならば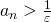 となるような自然数
となるような自然数 をとることができる。このとき、次のようにできる。
をとることができる。このとき、次のようにできる。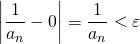
任意の
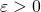 に対して、
に対して、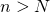 ならば
ならば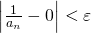 となるような自然数
となるような自然数 をとることができたので、数列
をとることができたので、数列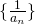 は値
は値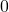 に収束する。
に収束する。(証明終わり)
-
(3)の解答
・一番強い(大きな数になる)項で分母分子を割ればよい。
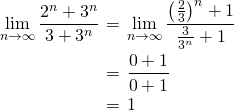
(下枠の定理を使った。)
指数関数と分数と収束
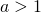 のとき、次の式が成り立つ。
のとき、次の式が成り立つ。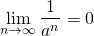
(証明)
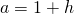 とおく。(
とおく。(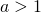 なので
なので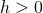 )
) 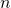 を自然数として、二項定理を使うと、
を自然数として、二項定理を使うと、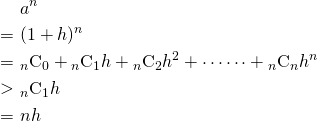
そして、任意の
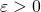 に対して、
に対して、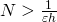 となるような自然数
となるような自然数 をとる。自然数
をとる。自然数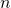 が
が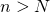 のとき、次のようにできる。
のとき、次のようにできる。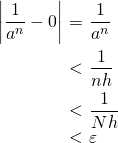
任意の
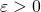 に対して、
に対して、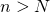 ならば
ならば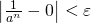 となるような自然数
となるような自然数 をとることができたので、数列
をとることができたので、数列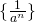 は値
は値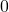 に収束する。
に収束する。(証明終わり)
二項定理
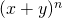 は次のように展開できる。
は次のように展開できる。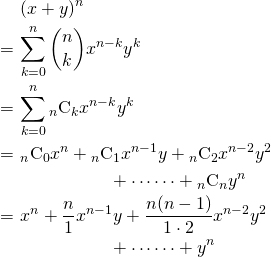
-
(4)の解答
・この問題は式に収束する数列が含まれており、ε-N論法を使わないとうまく解くことができない。数列が収束するということをε-N論法の定義によって書き直して解けばよい。
(i)
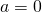 のとき
のとき数列
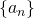 は収束するので有界であり、ある整数
は収束するので有界であり、ある整数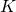 を用いて、
を用いて、 とすることができる。また、数列
とすることができる。また、数列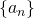 が
が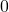 に収束するから、任意の
に収束するから、任意の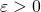 に対して、
に対して、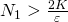 、かつ、
、かつ、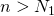 ならば
ならば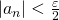 となるような自然数
となるような自然数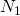 がとれる。
がとれる。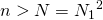 のとき、
のとき、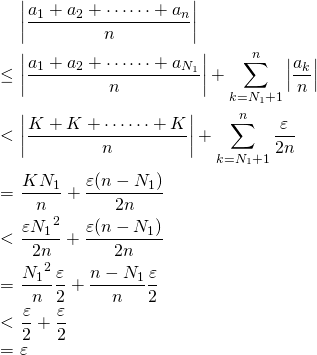
任意の
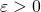 に対して、
に対して、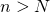 ならば
ならば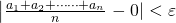 となるような自然数
となるような自然数 がとれたので、
がとれたので、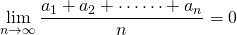
(ii)
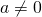 のとき
のとき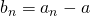 とおくと、
とおくと、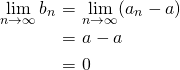
したがって、数列
 に(i)の結果が利用でき、
に(i)の結果が利用でき、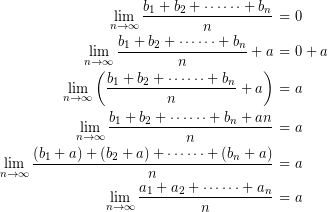
(i), (ii)より、