問題:次の計算をせよ。
![]()
中学校に進学し、算数という科目が数学という名前に変わると、数の世界に”負の数”というものが導入される。しかし、学校教育での”負の数”の導入は幾らか強引である。掛け算の計算規則は、大した説明もなしに丸暗記させられる。このページでは、学校教育で丸暗記される計算規則を、基礎的なところから考える。
“負の数”を数の世界に導入するにあたり、”負の数”の定義をしておきたい。すなわち、”負の数”というものは一体どんなものなのかということを、しっかりと決めておきたい。なぜなら、「負の数はこういうものだ、こういうものを負の数というんだ」ということを決めておくと、負の数が持つ性質を、その定義に基づいて考えることができるからである。明確な定義をしておけば、負の数を含む計算を、その定義に立ち返って考えることができる。
このページでは、負の数を次のように考える。
負の数の定義
正の数
 に対して、
に対して、(1)
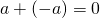
となる数を、負の数
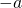 とする。
とする。例えば、正の数
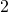 があれば、それに対応する負の数
があれば、それに対応する負の数 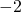 が存在し、これらを足し合わせると
が存在し、これらを足し合わせると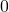 になる。また、負の数
になる。また、負の数 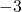 とあれば、これは正の数
とあれば、これは正の数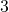 に対応する数であり、これらを足し合わせると
に対応する数であり、これらを足し合わせると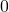 になる。
になる。日常世界にこの定義を当てはめた例を挙げる。例えば、正の数を持っているお金と定義する。こうすれば、負の数は、持っているお金と足し合わせて
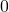 になる数であればよいから、背負っている借金と定義できる。
になる数であればよいから、背負っている借金と定義できる。数直線上での演算(足し算や引き算のこと)を考える。ここで、正の数の足し算を、数直線上の位置を右に数値分だけ動かす動作と定義する。こうすれば、負の数の足し算は、対応する正の数と足して
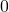 になるように定義すればよいから、左に数値分だけ動かす動作と定義できる。
になるように定義すればよいから、左に数値分だけ動かす動作と定義できる。
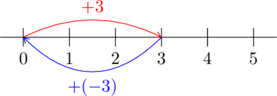
このように、正の数の足し算を数値分だけ右へ行く演算、負の数の足し算を数値分だけ左へ行く演算、と決めておくと、負の数の数直線を描くことができる。ある負の数
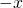 が、数直線上のどこに位置するのか知りたければ、
が、数直線上のどこに位置するのか知りたければ、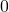 から左へ
から左へ だけ動かせばよい。例えば、
だけ動かせばよい。例えば、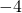 がどこに位置するのか知りたいならば、
がどこに位置するのか知りたいならば、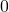 を起点にして、数値分の
を起点にして、数値分の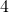 だけ左へ行けばよい。
だけ左へ行けばよい。
様々な数値を当てはめて位置を割り出していくと、次のような数直線ができる。

この数の順番は、一般的な数の順番と同じである。例えば、「今朝は
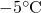 だった」と言えば、
だった」と言えば、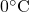 よりも
よりも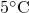 分だけ、寒かったわけである。これは、この数直線の考え方にそのまま当てはめることができる。温度計の数字は、この数直線と同じ順序で並んでいる。
分だけ、寒かったわけである。これは、この数直線の考え方にそのまま当てはめることができる。温度計の数字は、この数直線と同じ順序で並んでいる。どうやら、負の数を(1)のように定義すると、負の数は普段耳にする負の数と一致するようである。これで安心して足し算や引き算、掛け算や割り算といった、いわゆる四則演算をこの定義に基づいて考えることができる。
このページの構成は以下のようになる。
(1)負の数の足し算
(2)負の数の引き算
(3)負の数の掛け算
(4)負の数の割り算、0除算
-
負数の足し算
正の数
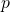 と負の数
と負の数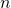 を使った足し算の組み合わせは次の4通りある。
を使った足し算の組み合わせは次の4通りある。(i)
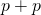
(ii)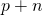
(iii)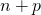
(iv)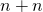
(i)
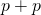 のとき
のとき(i)は、負の数を含まない計算なので、小学校で習ったようにして答えを出すことができる。
例:
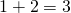
(ii)
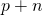 , (iii)
, (iii)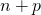 のとき
のとき(ii), (iii)は、正の数と負の数を一つずつ含む。足し算は、”足す数”と”足される数”を入れ替えても計算結果が変わらないので、(ii)から(iii)へ, (iii)から(ii)への変換が可能である。(加法の交換法則)
例:
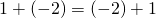
したがって、どちらか一方、例えば(ii)
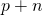 の場合のみを考えればよい。
の場合のみを考えればよい。ここで、”正の数を引くという操作”は、”負の数を足すという操作”に等しいことを示す。これを示すために、引き算を足し算の逆演算と定義する。すなわち、
 を足すという操作を
を足すという操作を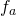 とするならば、
とするならば、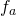 の逆演算
の逆演算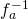 を
を を引く操作と定義する。ようするに、
を引く操作と定義する。ようするに、 として、引き算を定義する。
として、引き算を定義する。引き算の定義
(2)

このように定義すると、
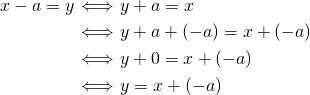
とでき、最初の式の右辺と最後の式の左辺が共に
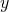 であるため、
であるため、![Rendered by QuickLaTeX.com \[x-a=x+(-a)~~~(=y)\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-e71809d04b6584da6b859b2ff935b7a5_l3.png)
である。これで、”正の数を引くこと”は、”負の数を足すこと”に等しいことが言えた。(ところで、これは直感的には当然のことである。数直線上で、正の数の引き算は左に数値分だけ移動させる操作であり、負の数の足し算も同じく左に数値分だけ移動させる操作なのだから)
正の数と負の数の足し算は、正の数同士の引き算に書き換えることが可能であると言えたので、次の例のように引き算として計算することができる。
例:
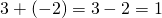
ところが、次の場合はどうだろう。引く数のほうが大きくなってしまい計算できない。(小学校ではこの計算は習わない)
例:
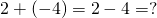
この計算は以下のような計算で全体を
 (マイナス)でくくることにより解決できる。
(マイナス)でくくることにより解決できる。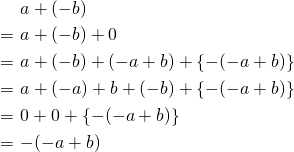
上の例は、
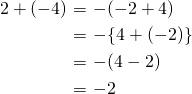
と計算できる。
(iv)
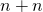 のとき
のとき以下のように計算することができる。
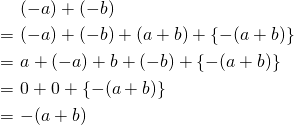
例:

-
負数の引き算
負の数の引き算を考える前に、負の数の定義(1)を拡張して、
 (マイナス)という記号に”逆元(ぎゃくげん)”を表すという新たな意味を加えたい。前項まで記号
(マイナス)という記号に”逆元(ぎゃくげん)”を表すという新たな意味を加えたい。前項まで記号 (マイナス)は、単に数字の前につけて負の数であることを表していたが、新たに、もとの数と足すと
(マイナス)は、単に数字の前につけて負の数であることを表していたが、新たに、もとの数と足すと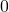 になるような数を表す、という意味を加えて再定義する。すなわち、次のように定義する。
になるような数を表す、という意味を加えて再定義する。すなわち、次のように定義する。逆元の定義
数
 に対して、
に対して、(3)
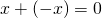
となるような数
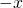 を、
を、 の逆元とする。
の逆元とする。これは、負の数の定義(1)の一般化(拡張)である。
 が正の数であれば、逆元
が正の数であれば、逆元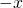 は(1)の定義通り負の数である。しかし、この定義では、
は(1)の定義通り負の数である。しかし、この定義では、 が正の数でないようなとき(負の数や
が正の数でないようなとき(負の数や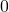 であるとき)も定義している。例えば、
であるとき)も定義している。例えば、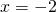 のときも定義されており、この逆元は
のときも定義されており、この逆元は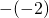 である。
である。ちなみに逆元の逆元は、もとの元(もとの数)になる。
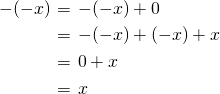
このことから、ある数に
 (マイナス)を付けるという操作は、
(マイナス)を付けるという操作は、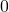 を中心に対称移動させることだと言える。
を中心に対称移動させることだと言える。
正の数
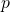 と負の数
と負の数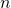 を使った引き算は次の2通りある。(
を使った引き算は次の2通りある。( は正負どちらでもよい数)
は正負どちらでもよい数)(i)
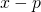
(ii)
(i)
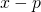 のとき
のとき負の数の定義(2)より、足し算に置き換えることが出来る。
例:
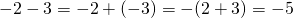
(ii)
 のとき
のとき(i)と同様に、足し算に置き換える。
![Rendered by QuickLaTeX.com \begin{eqnarray*} x-(-a)&=&x+\{-(-a)\} \\ &=&x+\{-(-a)\}+0 \\ &=&x+\{-(-a)\}+a+(-a) \\ &=&x+a+[-a+\{-(-a)\}] \\ &=&x+a+0 \\ &=&x+a \end{eqnarray*}](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-ac7f874becb0aa49ab28c40bdd1972fc_l3.png)
4行目から5行目への計算で、逆元の定義(3)を使った。
例:
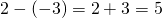
-
負数の掛け算
正の数
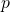 と負の数
と負の数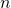 を使った掛け算は次の4通りある。
を使った掛け算は次の4通りある。(i)
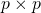
(ii)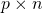
(iii)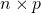
(iv)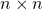
(i)
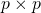 のとき
のとき(i)は、負の数を含まない計算なので、小学校で習ったようにして答えを出すことができる。
例:
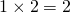
(ii)
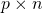 , (iii)
, (iii)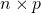 のとき
のとき掛け算の順序を換えても、式の値は変わらないので、(ii), (iii)のどちらか一方、例えば、(ii)の場合のみを考えればよい。
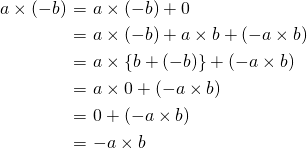
(注:
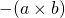 を
を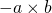 と書く)
と書く)例:
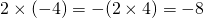
(iv)
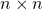 のとき
のとき以下のように計算できる。
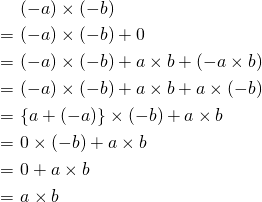
例:
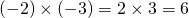 ・・・・・・(答え)
・・・・・・(答え) -
負数の割り算
掛け算の掛ける数
 が
が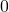 でないとき、割り算を、掛け算の逆演算と定義する。すなわち、次のように定義する。
でないとき、割り算を、掛け算の逆演算と定義する。すなわち、次のように定義する。割り算の定義
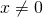 のとき、
のとき、(4)

正の数
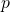 と負の数
と負の数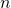 を使った割り算は次の4通りある。
を使った割り算は次の4通りある。(i)
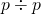
(ii)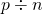
(iii)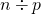
(iv)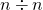
(i)
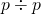 のとき
のとき(i)は、負の数を含まない計算なので、小学校で習ったように計算できる。
例:
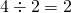
(ii)
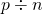 のとき
のとき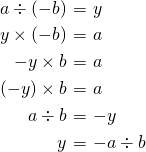
例:
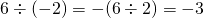
(iii)
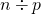 のとき
のとき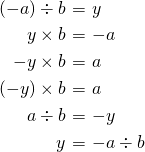
例:
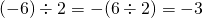
(iv)
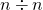 のとき
のとき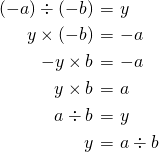
例:
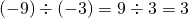
ところで、定義(4)の式の、
 を
を ,
,  を
を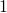 に書き換えると、
に書き換えると、![Rendered by QuickLaTeX.com \[y \times v = 1 \Longleftrightarrow 1 \div v = y\]](http://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-e61c791c479685f98b1c95e2d4f818a7_l3.png)
ここで、
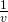 を、
を、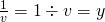 と定義すると、
と定義すると、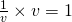
これを用いて、
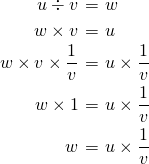
とできる。したがって、割り算は、
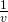 を使って、掛け算に書き直すことができる。これと
を使って、掛け算に書き直すことができる。これと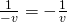 を使って、負の数を含む割り算の計算規則を、掛け算の計算規則から導くこともできる。
を使って、負の数を含む割り算の計算規則を、掛け算の計算規則から導くこともできる。0での割り算
定義(4)では、
 に
に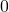 を含めなかったが、
を含めなかったが、 に
に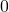 含めると、どうなるだろうか? 実は、以下のような理由で、
含めると、どうなるだろうか? 実は、以下のような理由で、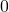 で割ることは定義できない。
で割ることは定義できない。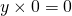 より、
より、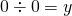 。したがって、
。したがって、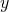 に好きな値を代入することにより、
に好きな値を代入することにより、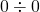 は、任意の値にできる。例えば、
は、任意の値にできる。例えば、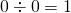 ,
, 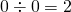 とできる。しかし、この
とできる。しかし、この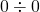 を認めてしまうと、
を認めてしまうと、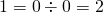 となり、
となり、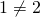 と矛盾する。したがって、
と矛盾する。したがって、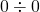 は定義できない。(
は定義できない。(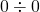 を普通の計算ができる数の仲間に入れてあげることができない)
を普通の計算ができる数の仲間に入れてあげることができない)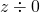 で、割られる数
で、割られる数 が
が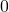 でないとき、すなわち、
でないとき、すなわち、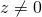 のとき、
のとき、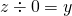

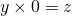 。 したがって、
。 したがって、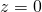 。 これは、
。 これは、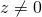 に矛盾する。よって、
に矛盾する。よって、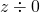 は、定義できない。(
は、定義できない。(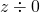 を普通の計算ができる数の仲間に入れてあげることができない)
を普通の計算ができる数の仲間に入れてあげることができない)