
-
このページでは、物体の位置から微分を使って、速度と加速度を定義する。その上で問題を解く。
このページの構成は以下のようになる。
(1)速度と加速度
(2)解答
-
物体の位置
物体の位置
 は、数直線上での位置を表す。例えば、
は、数直線上での位置を表す。例えば、 であれば物体が数直線上で
であれば物体が数直線上で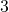 のところにあることを意味するし、
のところにあることを意味するし、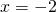 であれば物体が数直線上で
であれば物体が数直線上で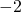 のところにあることを意味する。
のところにあることを意味する。
速度
平均の速度
ある時刻
 からある時刻
からある時刻 までに、位置が
までに、位置が から
から に変化したとき、時間
に変化したとき、時間 で位置が
で位置が 変わっている。このとき、平均の速度
変わっている。このとき、平均の速度 は次のように定義される。(
は次のように定義される。( は、変化した位置の量という意味で”変位”と呼ばれることがある)
は、変化した位置の量という意味で”変位”と呼ばれることがある)平均の速度
![Rendered by QuickLaTeX.com \[\bar{v} = \cfrac{\Delta x}{\Delta t}\]](https://sleep.oops.jp/wp-content/ql-cache/quicklatex.com-3b8be3e10466637f2d606a6671d88eeb_l3.png)
例えば、100mを10秒で走ったとき、この10秒間の平均の速度は、
 , したがって、”走った方向に10m/s”である。
, したがって、”走った方向に10m/s”である。注:速度は大きさと向きを持ったベクトル量なので、方向も明記しておく必要がある。
 の値が+ならば、その向きは数直線の+の方向である。もし走った方向と逆に数直線をとったならば、
の値が+ならば、その向きは数直線の+の方向である。もし走った方向と逆に数直線をとったならば、 となる。しかし、この場合でも、速度の向きは、数直線の向きと逆の向きなので、同じく”走った方向”となる。
となる。しかし、この場合でも、速度の向きは、数直線の向きと逆の向きなので、同じく”走った方向”となる。瞬間の速度
平均の速度の時間間隔
 を限りなく
を限りなく に近づけると、瞬間の速度となる。単に速度といった場合は、瞬間の速度を意味する。例えば、位置が関数
に近づけると、瞬間の速度となる。単に速度といった場合は、瞬間の速度を意味する。例えば、位置が関数 で与えられているとき、時間
で与えられているとき、時間 での速度
での速度 は、
は、
2行目の
 からわかるように、瞬間の速度
からわかるように、瞬間の速度 は位置
は位置 を
を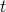 で微分したものである。
で微分したものである。瞬間の速度

これらの式は、書き方が異なるだけで同じ意味、すなわち、
 の
の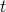 微分を意味する。
微分を意味する。加速度
加速度
 は、速度
は、速度 を時間
を時間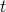 で微分したものである。したがって、加速度
で微分したものである。したがって、加速度 は、位置
は、位置 を時間
を時間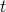 で二回微分したものである。
で二回微分したものである。(瞬間の)加速度

これらの式は、すべて同じ意味、すなわち、
 の
の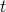 微分(もしくは
微分(もしくは の二回微分)を意味する。
の二回微分)を意味する。 -
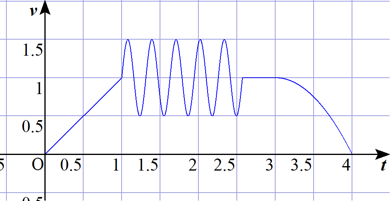
加速度と時間のグラフ
加速度
 は、速度
は、速度 の微分だから、与えられた式を微分すればよい。
の微分だから、与えられた式を微分すればよい。
これをグラフにすると次のようになる。
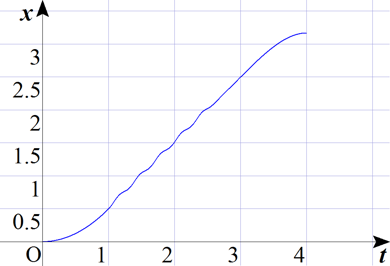
位置と時間のグラフ
速度
 は、位置
は、位置 を微分したものである。速度
を微分したものである。速度 から、位置
から、位置 を求めるには、
を求めるには、 を微分の逆演算である積分によって求めればよい。積分定数は
を微分の逆演算である積分によって求めればよい。積分定数は の値が連続となるように決める。
の値が連続となるように決める。
これをグラフにすると次のようになる。
(解答終わり)